لتوضيح ذلك أكثر، نوضح الآن كيفية المعادلة (4) يؤدي إلى التشابك في نسخة من تجربة فاينمان. توزيعان كرويان للكتلة، لكل منهما كتلة إجمالية م ونصف القطر ر، يتم إعدادها في تراكب كمي لموقعين. ويمكن تحقيق ذلك، على سبيل المثال، من خلال تنفيذ مقسمات شعاع المادة والموجة6، التلاعب بالإمكانيات32 أو استغلال درجات الحرية الداخلية، مثل السبينات الكمومية في تجارب ستيرن-جيرلاخ5 (تين. 3). يُفترض أن الجاذبية هي التفاعل الوحيد بين الجسيمات، وفي الحد غير النسبي ووصف المادة ضمن التكميم الأول، فإنها تعمل فقط كمرحلة كمومية وأناي ≔ زم2ر/(ح دأناي) على كل فرع تراكب5,6، أين دأناي هي المسافة بين توزيعات المادة في الفرع المسمى بـ أنا, ي ∈ {ل، ص}، و زم2/دأناي هي طاقة الوضع النيوتونية. مع حجم التراكب Δس أكبر بكثير من أصغر مسافة درل، فقط المرحلة الكمومية و ≔ ورل مهم، بحيث تكون الأنظمة متشابكة بشكل واضح، ويعتمد التشابك عليها فقط و (المراجع. 5,6).
على النقيض من ذلك، عندما Δس ≪ درل، تصبح المعلمة ذات الصلة بالتشابك بشكل أساسي (overline{varphi }:= varphi ,Delta {x}^{2}/{d}_{{rm{RL}}}^{2})(المرجع. 33). لقياس التشابك، يمكن إعادة تجميع المسارات المتراكبة والبحث عن الارتباطات بين مخرجات مقياس التداخل6 أو درجات الحرية الداخلية5.
توزيعان للكتلة الكروية (1 و 2) لنصف القطر ر يتم وضعها في تراكبات كمومية في موقعين كحالات N00N، حيث يشير اللون الأزرق والأحمر إلى المكونات المفصولة بـ Δس. بعد تفاعل الجاذبية لفترة قصيرة، يتم إعادة دمج المسارات والبحث عن التشابك5,6. على الرغم من توضيح قياس تداخل ستيرن-جيرلاخ مع الدوران الداخلي5، من الممكن أيضًا إنشاء إعدادات بديلة، مثل Mach–Zehnders المتوازي6. هنا، Δس يصور أكبر من الحد الأدنى للفصل درل، ولكن يمكن تنفيذ التكوين العام، بما في ذلك Δس ≪ درل.
الجاذبية الكمومية
نقوم الآن بتحليل هذه التجربة باستخدام الجاذبية الكمومية المضطربة مع وصف QFT للمادة. مع تجاهل التفاعلات الكهرومغناطيسية، فإننا نأخذ الحالة الأولية للأشياء مباشرة بعد وضعها في تراكب كمي كمنتج لحالات N00N:
$$begin{array}{l}|varPsi rangle =frac{1}{2}({|Nrangle} _ {{rm{1L}}}{|0rangle }_ {{rm{1R}}}{|uparrow rangle } _ {1} + {|0 rangle} _ {{ rm {1L}}} {|N rangle } _ {{ rm {1R}}} {| downarrow rangle } _ {1}) qquad otimes ({|Nrangle) } _ {{ rm {2L}}} {|0 rangle} _ {{ rm {2R}}} {| uparrow rangle} _ {2} + {|0 rangle} _ {{ rm {2L}}} {|N rangle } _ {{ rm {2R}}} {|downarrow rangle} _ {2})،end{array}$$
(5)
حيث |ن⟩السيدأنا هو منتج من ن حالات الوضع المستقل لجسيمات المادة التي تخضع لحقل عددي معقد34، مع السيد ∈{1، 2} و أنا ∈ {L، R} وضع علامات على موضع الأجسام الكروية (مطابقة الشكل 1). 3). ن هو عدد الجزيئات الموجودة في الأجسام، بحيث م= من ، مع مكتلة الجزيئات. نقوم أيضًا بتضمين حالات الدوران الداخلية المحتملة {|↑⟩ |↓⟩}، والتي يمكن استخدامها لتوليد التراكبات الكمومية.
بعد وقت ر حالة نظام المادة في صورة شرودنغر هي
$$| varPsi
(6)
أين (وايدهات{T})هو مشغل ترتيب الوقت، رهو متغير زمني وهمي، ({widehat{H}}_{0})هو هاميلتون الجاذبية الكمومية المضطربة في غياب تفاعلات المادة والجاذبية ({widehat{H}}_ {{rm{I}}}:= exp ({rm{i}}{widehat{H}}_{0}t/hbar ){widehat{H}}_ {{rm{int}}},exp (-{rm{i}}{widehat{H}}_{0}t/hbar )). قبل أن يتم إعادة شراء مسارات التراكب معًا، على سبيل المثال من خلال عكس Stern-Gerlachs1,5، يمكننا أن نكتب
$$begin{array}{l}|,varPsi
(7)
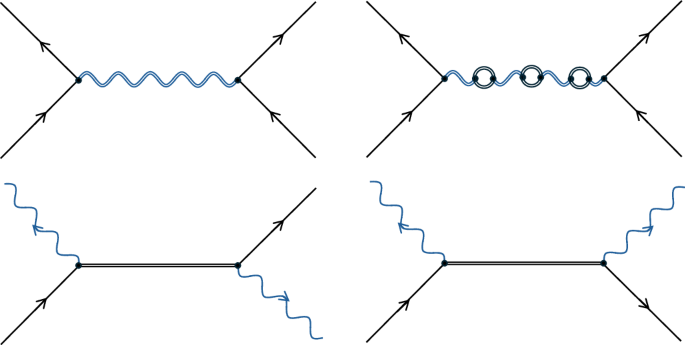
أين ({alpha} _ {ij}in {mathbb{C}}) . لقد أهملنا الآن أي حالات دوران داخلية وحالات الفراغ من أجل البساطة. يمكننا حساب السعاتأأناي عن طريق أخذ المنتج الداخلي للمعادلة (7) (وكذلك المعادلة (6)))، مع حالات الأساس |ن⟩1أنا|ن⟩2 ي وتوسيع العملية الوحدوية المرتبة زمنياً في المعادلة (6) مثل سلسلة دايسون26,35. يمكن بعد ذلك كتابة السعات كسلسلة مضطربة بحيث يتوافق كل مصطلح مع سلسلة دايسون: ({alpha}_{ij}={alpha}_{ij}^{(0)}+{alpha }_{ij}^{(1)}+{alpha}_{ij}^{(2)}+cdots ,) . العملية الأولى التي يتم فيها تبادل الجرافيتون الافتراضي بين الأجسام المادية تحدث في المرتبة الثانية في السلسلة وتتوافق مع مخطط فاينمان في الشكل. 1 (أعلى اليسار). سعة مخطط فاينمان هذا، ضمن تقريب جيد جدًاجر ≫ دأناي (طُرق)، يكون
$$frac {G{M}^{2}t}{hbar {V}^{2}}iint {{ rm {d}}} ^ {3} { bf {x}} ، {{ rm {d}}} ^ {3} { bf {y}} frac {{ ثيتا } _ {1i} ({ bf {x}}) { theta} _ {2j} ({ bf {y}})} {| {bf{x}}-{bf{y}}| }equiv {varphi} _{ij},$$
(8)
أينأناالسيدأنا(س)≔ أنا ( ر–∣س– Xالسيدأنا∣ ) هي دالة خطوة الوحدة التي تحدد الشكل الكروي لتوزيع المادة السيدفي فرع أنا,Xالسيدأنا هو إحداثيات مركز الكتلة للتوزيعات وV ≔ 4 صر3/3. السعة المذكورة أعلاه تساهم بشكل مباشر في ({alpha }_{ij}^{(2)})))))))))))))))))})})})بحيث أنه عندما Δس ≫ درل، ال ({alpha} _ {{rm{RL}}}^{(2)}) السعة تهيمن على كل الآخرين ويساوي أنا و. ثم نظرا لذلك ({alpha} _ {i x jeo}^<)}=1)من سلسلة دايسون وذلك ({ألفا } _ {ij} ^ {(1)}))))))))))))))))))))))))}))}) لا يحتوي على تقلصات في مجال الجاذبية، ويتبقى لنا أأناي≈ 1 باستثناءأرل≈ 1 + ط و، والذي يطابق النتيجة الكمية الأولى من الدرجة الأولى في المرحلة الكمومية (exp ({rm{i}}varphi )) . يتم الحصول على النتيجة الكاملة غير المضطربة بشكل مباشر من خلال النظر في شكل مخططات فاينمان ذات الترتيب الأعلى المقابلة واستقراء النتيجة26.
الجاذبية الكلاسيكية
نحن الآن نعتبر التجربة المذكورة أعلاه ضمن سياق الجاذبية الكلاسيكية. الحساب يتبع ما سبق ولكن مع تفاعل هاميلتوني للمعادلة (4) بدلا من المعادلة (2). في المرتبة الثانية في سلسلة دايسون لا توجد انقباضات ويك غير متلاشية تتوافق مع مخططات فاينمان التي تحتوي على اتصال كمي بين الأجسام المادية، والمخطط المسؤول عن التشابك في الجاذبية الكمومية، الشكل 1. 1 (أعلى اليسار)، يصبح الشكل. 2 (الوسط العلوي). يمثل هذا الرسم البياني الجسمين الماديين الموجودين في مجال الجاذبية الكلاسيكي المشترك لهما، حيث تساهم السعة فقط في مرحلة كمومية نسبية محلية بين فروع كل جسم مادي، وهو ما لا يؤدي إلى التشابك13. ومع ذلك، في الترتيب الرابع في السلسلة، يظهر رسم تخطيطي حيث يتم توصيل توزيعات المادة ميكانيكيا الكم من خلال جسيمات المادة الافتراضية (الشكل 1). 2، أعلى اليمين). ضمن نفس التقريبات كما في حالة الجاذبية الكمومية، فإن سعة مخطط فاينمان هي (طُرق)
$$ {{vartheta}}_{ij}:= frac {{m}^{6}{t}^{2}{N}^{2}}{4{{rm{pi }}}^{2}{hbar }^{6} {V} ^ {2}} { left (i int {{ rm {d}}} ^ {3} { bf {x}} {{ rm {d}}} ^ {3} { bf {y}} frac { varPhi ({ bf {x}}) varPhi ({ bf {y}}) { theta} _ {1i} ({ bf {x}}) { theta} _ {2j} ({ bf {y}})} {| {bf{x}}-{bf{y}}| }يمين)}^{2},$$
(9)
أينف(س) ≔- ج2ح00(س)/2 هو إجمالي إمكانات الجاذبية للأشياء المادية، و ϑأناي يساهم بشكل مباشر في ({alpha} _ {ij}^ {(4)}) في المعادلة (7). كما لدينا نظرية كلاسيكية للجاذبية، ف(س) هو نفسه في كل فرع من فروع التراكب، وإلا فإن القوة النيوتونية ستكون في حالة تراكب كمي. اعتبرت بعض الأعمال أن الجاذبية هي أمر كلاسيكي ولكنها لا تزال تسمح للمجال أو القوة النيوتونية أن تكون في حالة تراكب كمي.36,37,38,39. هنا، نتمسك بفكرة أن التراكب الكمي هو ظاهرة ميكانيكية كمومية بحتة بحيث ف(س) غير متراكب في المعادلة (9) وليس مشغل الكم. ومع ذلك، على الرغم من هذا، المعادلة (9) بشكل عام يؤدي إلى التشابك، كماأنا1 أنا(س) وأنا2 أنا(س) تختلف بالنسبة لمسارات التراكب المختلفة وترتبط من خلالها∣س-ذ∣، مثل ذلك ({alpha} _ {ij}^ {(4)})يختلف لكل مسار تراكب، باستثناء ({alpha} _ {{rm{LL}}}^{(4)}={alpha} _ {{rm{RR}}}^{(4)})من التماثل. يمكننا أن نفهم هذا من مخطط فاينمان في الشكل.
2 (أعلى اليمين)، حيث، على عكس إمكانات الجاذبية، تدخل جسيمات المادة الافتراضية في تراكب كمي مع حالات كتلة مختلفة وتختلف المسافة التي تنتشرها جسيمات المادة الافتراضية في كل فرع، مما يؤدي إلى التكاملات المكانية في المعادلة (9) يتم الاتصال من خلال ∣س-ذ∣.
مثل ف (س) يأتي من تراكب المادة في المعادلة (9)، يجب علينا أن نفكر بالضبط في كيفية الحصول على الجاذبية من المادة الكمومية في النظرية الأساسية للجاذبية الكلاسيكية. في النهج الأكثر اعتبارا40,41, ف(س) في المعادلة (9) هو مجموع متوسط إمكانات حالات التراكب للكائنين. في هذه الحالة، ϑأناي يتناسب عكسيا معدأناي بحيث إذا كان Δس ≫ درل ، فإن سعة RL تهيمن على جميع الآخرين وهي كذلك∣ϑرل∣≈ ϑ، أين (طُرق)
$$sqrt {{vartheta}}=frac{6}{25}frac {{G}^{2}{m}^{2}{M}^{3}Rt}{{hbar }^{3}{d} _ {{rm{RL}}}}.$$
(10)
الحالة في المعادلة (7) ومن ثم يصبح متشابكًا بشكل واضح، لأنه، تمامًا كما هو الحال في الجاذبية الكمومية، أرليحتوي على مساهمة ϑوهذا ليس في أي من السعات الأخرى أأناي. علاوة على ذلك، مثل الجاذبية الكمومية33، التحجيم العكسي ل ϑأناي معدأناي يسمح (overline{{vartheta }}:= {vartheta},Delta {x}^{2}/{d} _ {{rm{RL}}}^{2})ليتم تحديدها على أنها المعلمة ذات الصلة للتشابك عندما Δس ≪ درل.
نشر لأول مرة على: www.nature.com
تاريخ النشر: 2025-10-22 03:00:00
الكاتب: Joseph Aziz
تنويه من موقع “yalebnan.org”:
تم جلب هذا المحتوى بشكل آلي من المصدر:
www.nature.com
بتاريخ: 2025-10-22 03:00:00.
الآراء والمعلومات الواردة في هذا المقال لا تعبر بالضرورة عن رأي موقع “yalebnan.org”، والمسؤولية الكاملة تقع على عاتق المصدر الأصلي.
ملاحظة: قد يتم استخدام الترجمة الآلية في بعض الأحيان لتوفير هذا المحتوى.
موقع "yalebnan" منصة لبنانية تجمع آخر الأخبار الفنية والاجتماعية والإعلامية لحظة بلحظة، مع تغطية حصرية ومواكبة لأبرز نجوم لبنان والعالم العربي.