Participants and stimuli

fMRI data were taken from 174 participants of the HCP movie-watching dataset⁵¹. The sample consisted of 104 female and 70 male individuals (mean age 29.3 years, s.d. = 3.3) born in Missouri, USA. In total, 88.5% of the sample identified as ‘white’ (4.0% Asian, Hawaiian or Other Pacific Island; 6.3% Black or African American; 1.1% unreported). The English language comprehension ability of the sample (as assessed by age-adjusted NIH Picture Vocabulary Test⁵² scores) was above the national average of 100 (mean = 110, s.d. = 15). The participants were scanned while watching short (ranging from 1 to 4.3 min in length) independent and Hollywood film clips that were concatenated into four videos of 11.9–13.7 min total length. Before each clip, and after the final clip was displayed, there were 20 s periods in which there was no auditory stimulation and only the word ‘REST’ presented on the screen. There were four separate functional runs, in which observers viewed each of the four separate videos. All four videos contained an identical 83 s ‘validation’ sequence at the end of the video that was later removed to ensure independent stimulation in each cross-validation fold. Audio was scaled to ensure that no video clips were too loud or quiet across sessions and was delivered by Sensimetric earbuds that provide high-quality acoustic stimulus delivery while attenuating scanner noise. The participants also took part in one hour of resting state scans, also split into four runs of equal (around 15 min) length. Full details of the procedure and the experimental setup are reported in the HCP S12000 release reference manual⁵³. The ethical aspects of the HCP procedures were approved by Washington University Institutional Review Board (IRB) (approval number 201204036) and all use of the data reported in this manuscript abide by the WU-Minn HCP Consortium data use terms.

HCP data format and preparation

Ultra-high field fMRI (7 T) data from the 174 participants were used, sampled at 1.6 mm isotropic resolution and a rate of 1 Hz (ref. ⁵¹). Data were preprocessed identically for video watching and resting state scans. For all analyses, the FIX-independent-component-analysis-denoised time-course data, sampled to the 59,000 vertex-per-hemisphere through the areal feature-based cross-participant alignment method (MSMAll)⁵⁴ surface format was used. These data are freely available from the HCP project website. The MSMAII method is optimized for aligning primary sensory cortices based on variations in myelin density and resting state connectivity maps¹⁸. Owing to the unreliable relation between cortical folding patterns and functional boundaries, MSM method takes into account underlying cortical microarchitecture, such as myelin, which is known to match sensory brain function better than cortical folding patterns alone⁵⁵. Previous research has demonstrated that such an approach improves the cross-participant alignment of independent task fMRI datasets while at the same time decreasing the alignment of cortical folding patterns that do not correlate with cortical areal locations⁵⁴.

We applied a high-pass filter to the timeseries data through a Savitzky Golay filter (third order, 210 s in length), which is a robust, flexible filter that allowed us to tailor our parameters to reduce the influence of low frequency components of the signal unrelated to the content of the experimental stimulation (for example, drift, generic changes in basal metabolism). For each run, BOLD time-series data were then converted to percentage signal change.

For purposes of cross-validation, we made training and test datasets from the full dataset. We removed the final 103 s of each functional run, which corresponded to the identical ‘validation’ sequence and final rest period at the end of each video run. Our training dataset therefore consisted of the concatenated data from the four functional runs with this final 103 s removed from each. The test dataset was created by concatenating the final 103 s from each run into a 412 s set of data.

All connective-field models were fit on the individual-participant data and for video watching these models were also fit to the data of an across time-course averaged (HCP average) participant. Split-half participant averages (n = 87) were also created through a random 50% split of individual-participant data. Split-half video averages were created by creating separate datasets based on the first (videos 1 and 2) and second half (videos 3 and 4) of the videos.

Dual-source connective-field model

Model maps of V1 and S1 topography

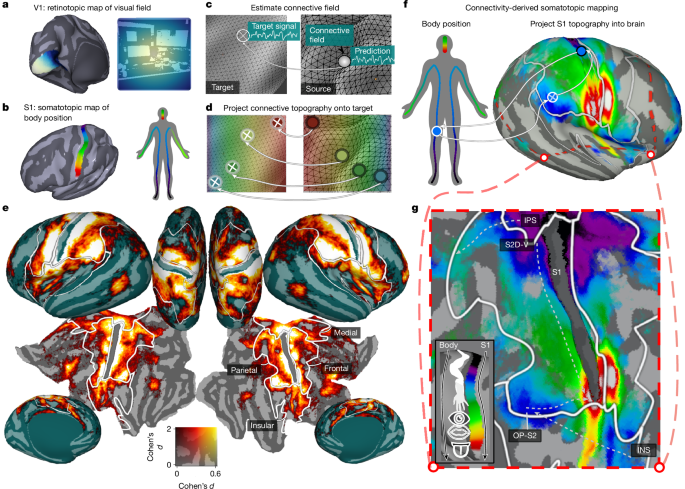
Our analyses extend the approach of connective-field modelling, wherein responses throughout the brain are modelled as deriving from a ‘field’ of activity on the surface of a ‘source’ region—classically V1. In turn, preferences for positions on the visual field can be estimated by referencing the estimated connective-field V1 positions against the retinotopic map of V1 (Fig. 1a–c). Here we extend this approach by simultaneously modelling brain responses as deriving from connective fields on both the V1 and S1 surfaces. This requires defining both a V1 and S1 source region and their underlying topographic maps.

To define these V1 and S1 source regions, we defined subsurfaces (one for each hemisphere) from the full cortical mesh, containing the vertices of a multimodal parcellation of the HCP data for regions V1 and Brodmann area 3b¹⁸. We chose region 3b as it is the first cortical input stage for tactile processing and is the most topographically organized subregion of S1.

To provide a model retinotopic map for V1, we used data from a ‘retinotopic prior’ that defines participant-averaged parameters of preferred visual field position (eccentricity, polar angle) estimated from a population receptive field (pRF) analysis of the HCP data⁵⁶. Thus every vertex in V1 was associated with an eccentricity and polar angle value that defined its preference for the corresponding position in the visual field. Using this data, the V1 subsurface was then curtailed to only include vertices within the region stimulated by the video display (within 8 degrees of visual angle (DVA) from the fovea).

The known topographic organization of S1 is a somatotopic map, which is an approximately dorsomedially to ventrolaterally oriented gradient that runs from sensitivity to lower limbs to the upper limbs and face¹³. To provide a continuous coordinate space for this somatotopic gradient, for each vertex, we calculated the geodesic distance from the vertices at the most dorsomedial edge of the 3b subsurface.

Design matrix

We first summarized the V1 and S1 subsurfaces as a finite set of spatial profiles by deriving eigenfunctions of their Laplace–Beltrami operator (LBOEs) using functions contained within Pycortex⁵⁷. This decomposition, referred to as recovering the shape DNA of a manifold, yields a finite family of real-valued functions that are intrinsic to the surface shape, orthogonal and ordered according to spatial scale^58,59 (Extended Data Fig. 1a). In principle, one can approximate any arbitrary spatial pattern on the surface (that is, a connective field) through a linear combination of LBOEs.

To validate this approach and determine the number of LBOEs to use in our analysis, we conducted pilot analyses where we attempted to predict target Gaussian connective fields of varying sizes from linear combinations of LBOEs. These analyses indicated that for both V1 and S1, 200 LBOEs were sufficient to adequately predict connective fields with a sampling extent of 2 mm, which approximates the lower bound of the known sampling extent of extrastriate cortex from V1 (that is, in V2)¹⁴. Reconstruction performance was at near-ceiling levels for sampling extents of 4 mm and above (Extended Data Figs. 2 and 3) and increasing the number of LBOEs from 200 led to trivial increases in reconstruction performance relative to the increases in computation time. Furthermore, visualizing the performance of a 200 LBOE model in predicting connective fields centred on each V1 and S1 vertex revealed no systematic spatial inhomogeneities (Extended Data Figs. 2 and 3). As such we opted to use 200 LBOEs per subsurface in our connective-field modelling.

With this approach validated, we generated model time courses for our design matrix via the dot product of the time-course data corresponding to each subsurface and each of the 200 corresponding LBOEs. Each model time course therefore reflects the sum of the timeseries data within the subsurface, weighted by one of the LBOEs (Extended Data Fig. 1b). The model time courses were then z scored over time and stacked to form a design matrix for model fitting. Thus, there were 800 regressors in our design matrix: 400 from V1 and 400 from S1 (200 per hemisphere), which were used to explain the BOLD responses during resting-state and video watching.

Model fitting

All model fitting was conducted in Python, exploiting the routines implemented by the ‘Himalaya’ package⁶⁰. In ordinary least-squares (OLS) regression, one estimates weights b, such that data y are approximated by a linear combination of regressors Xb (Extended Data Fig. 1c). Here we used banded ridge regression, which belongs to a family of regularized regression techniques that estimate a regularization parameter λ to improve the generalization performance of OLS regression⁶¹. Banded ridge regression expands on these techniques by estimating a separate λ for separate feature spaces i of the design matrix X—thereby optimizing regularization strengths independently for each feature space (Extended Data Fig. 1d). Banded ridge regression therefore respects the fact that different feature spaces in the design matrix may differ in covariance structure, number of features and prediction performance—entailing different optimal regularization.

In the present case, our two feature spaces consisted of the visual and somatosensory modalities or, equivalently, the 400 V1 and S1 model time courses (X_v1, X_s1) described in the previous section. Thus, to model brain activity of a particular voxel, banded-ridge regression computes the weights b*_i, as defined below:

Similarly to unbanded ridge regression, the ridge weights b*_i are estimated from the training data and the hyperparameters λ_i are learned through cross validation. In the present case, our training data consisted of four runs of functional data in which the participants watched an independent video. This natural organization of the data enabled us to use a leave-one-video-out cross-validation strategy to estimate λ_i.

Connective-field estimation

For a given voxel, the coefficients b*_i estimated by the banded ridge regression model can be interpreted as the cross-validated importance of each model time course in the design matrix in explaining its response throughout the experiment (rest or video watching). By extension, as each model time course derives from an orthogonal spatial profile on the surface of V1 or S1, this means that b*_i also implicitly estimates the importance of each of the underlying spatial profiles. Accordingly, for any given voxel, the dot product of its estimated b*_i and the corresponding spatial profiles s_i reveals a spatial map of the importance of each vertex on S1 and V1 in explaining the voxels response—or equivalently—it estimates its visual and somatosensory ‘connective field’ (Extended Data Fig. 1e).

Notably, this method of connective-field estimation is more flexible than ‘classic’ connective-field estimation procedure as it removes the constraint that the connective-field profile is a Gaussian defined by a centre (V₀) and extent (σ), and can estimate non-canonical or irregular spatial patterns that do not resemble unimodal and circularly symmetric Gaussians.

Furthermore, this form of connective-field modelling through banded ridge regression is highly extensible as it can incorporate additional source regions with different topographic formats (for example, primary motor cortex, primary auditory cortex) simply through expansion of the feature spaces and bands in the design matrix. Banded ridge regression is particularly suitable in this context of multiple, potentially correlated feature spaces, as the estimation of multiple regularization parameters also leads to implicit feature selection⁶⁰. During cross-validation, banded ridge regression is able to learn to ignore some feature spaces to improve generalization performance. To ignore an uninformative feature space, banded ridge regression penalizes its influence by assigning a large regularization hyperparameter λ_i, implying that the coefficients b*_i are shrunk toward zero. This process effectively removes uninformative feature spaces from the model.

We note that great care should be taken when interpreting connective-field modelling outcomes in regions directly abutting the source region. This is because results in these neighbouring regions are likely to be biased by partial-voluming effects: in this case, a connective field centred in the source region spuriously samples from the neighbouring target region itself across the border. This contamination can be due to several factors, among which the fact that single voxels can sample grey matter on both sides of the boundary on the surface (or across both banks of a sulcus), the broad scale of spatial autocorrelations of the underlying responses and the BOLD point-spread of around 2 mm, more than the voxel size in the acquisitions used here.

Connectivity-derived retinotopic and somatotopic mapping

With connective-field profiles estimated for each vertex, preferred visual field and body positions were estimated by taking the dot product of each S1 and V1 connective field and the corresponding somatotopic and retinotopic map (see the ‘Model maps of V1 and S1 topography’ section) and then dividing by the sum of the connective fields (Extended Data Fig. 1f). As the values of the connective-field profile represent the importance of each location on the source region in explaining a given voxels response, this is akin to a weighted averaging, whereby the retinotopic/somatotopic maps are averaged in a manner weighted by the predictive performance at each location.

To validate the ability of our model to simultaneously estimate retinotopic and somatotopic maps, we compared our connective-field-derived maps to independent maps derived from exogenous stimulation. For an exogenously derived retinotopic map, we leveraged the retinotopic prior previously described⁵⁶. To obtain an exogenously derived somatotopic map, we used data from an independent, publicly available whole-brain somatotopy dataset collected at 3 T, where 62 participants performed movements with 12 discrete body parts ranging from toe to tongue^19,62. The participant-wise β weights for each of 12 body parts were nearest-neighbour resampled into the same 59,000 vertex per hemisphere space as the HCP data. We then conducted a second-level GLM on these beta weights and then took the dot-product of the resulting group-average betas and their ordinal position on the S1 homunculus, resulting in a continuous toe–tongue metric of body part sensitivity. Note that, before the dot product operation, we averaged the leg β weight across left and right leg movements, as only this body part was represented bilaterally in the dataset.

Correlating our connectivity-derived topographic maps with these exogenous maps, we confirm that our outcomes recovered detailed somatotopic and retinotopic organization that closely mirrors those derived from exogenous stimulation. Notably, even in medial and insular regions, where the performance of the connective-field model is relatively low, many features of the exogenously derived somatotopic maps are clearly present in our own (Extended Data Fig. 5e–h).

Analysis of subfields within S1

To explicitly relate our connective-field coordinates to body parts, we leveraged the definitions of four topographic body part fields within our S1 source region (3b) provided previously¹⁸ (lower limb, trunk, upper limb and face), which were identified on the basis resting-state functional connectivity gradients and somatotopic mapping task contrasts. Note that these authors¹⁸ also report the existence of an additional eye field in some areas of sensorimotor cortex, but indicate that this is not reliably identifiable in area 3b; thus, this does not feature in our analysis. We corroborated the validity of these four subfields with data from the whole-brain somatotopy dataset described in the previous section. The second-level random effects GLM analysis was used to derive the S1 positions corresponding to the peak of the group-level t statistic for each body part. These data, alongside the topographic field boundaries, are shown in Extended Data Fig. 4d. All functionally defined peak statistics fell within the corresponding body part field defined in that study¹⁸.

With these fields defined, for each vertex, we summed the connective-field profile within each field and then normalized by the sum across all fields to estimate the proportion within each field. This measure therefore provides an estimate of the importance of each body part field in driving responses within the vertex, which we then compared between somatosensory regions of interest (Extended Data Fig. 4e).

Model performance metrics

The dual specification of our model with multiple feature spaces also enables us to disentangle the contribution of each feature space (sensory modality) to overall prediction performance. Specifically, variance decomposition through the product measure enables the computation of independent R² scores per feature space that sum to the total R² of the dual model.

Where ({hat{y}}_{i}) is the subprediction computed on feature space X_i alone, using the weights b*_i of the dual model. To evaluate out-of-sample performance of the model, the parameters estimated from the training data were then used to predict the test data and the variance explained from the V1 and S1 feature spaces was evaluated using the above formula.

ROI definitions

Classically somatotopic ROIs

To define somatotopic regions of interest, we leveraged a previously defined, gross anatomical parcellation of parietal, medial, insular and frontal zones that have been found to contain robust homuncular somatotopic gradients, or ‘creatures’ of the somatosensory system¹³. These ‘creatures’ were themselves defined by a combination of regions in the multimodal parcellation of ref. ¹⁸, of which the voxel-averaged response to tactile stimulation was significantly above zero. Further details of the exact regions of the Glasser parcellation¹⁸ that correspond to each ROI can be found in another paper¹³. granular regions of somatotopic cortex reported in the main text (3a, Brodmann area 1–2) were defined from individual Glasser atlas definitions. Other broader regions reported are combinations of multiple Glasser atlas regions: SII (OP1 and OP4) superior parietal lobule (7Am, 7PL, 7PC, 7AL, 7Pm, 7 M, VIP, MIP, LIPd, LIPv) inferior parietal lobule (PF, PFm, PFt, PGa, PGp PFop, PFcm).

Classically visual ROIs

To define visual ROIs, we used a pre-existing probabilistic atlas of 25 retinotopic visual regions provided in ref. ²⁶. To this parcellation, we added the regions FFA, FBA, EBA and PPA, which were defined by functional localizer (floc) data taken from the NSD³⁵. Specifically, the participant-averaged t-statistics for the faces/bodies versus all other stimulus categories contrast were thresholded at the α < 0.05 level and ROIS were hand-drawn using pycortex. Note therefore, that we opted to not use the pre-drawn definitions packaged with the NSD dataset, which were defined according to a liberal t > 0 thresholding. Our definition of the EBA overlaps with the ref. ²⁶ atlas regions LO2, TO1 and TO2; thus, only the EBA is displayed on cortical flatmaps to avoid overplotting. The relationship between these regions is shown in Extended Data Fig. 6a.

Statistical testing

Topographic connectivity scores

To generate a measure of topographic connectivity, the out-of-set R² values for visual and somatosensory connective-field predictions were corrected for the R² of a non-topographic null model, of which the predictions were generated through the mean V1 and S1 time courses, respectively. This means that, although the corrected values are no longer interpretable as variance explained, they reflect the superiority of the generalization performance of a spatial connective-field model relative to a non-spatial model. This correction therefore conservatively assesses the presence of true topographic connectivity by referencing against an explicit null model. One-sample t-tests were conducted to compare these corrected scores against zero and reported P values are two sided. To provide estimates of the magnitude of topographic connectivity, we computed the effect size Cohen’s d_z through the formula:

The within-participant differences in topographic connectivity scores were analysed using repeated-measures ANOVA, implemented in the afex package in the R programming language⁶³. In modelling pairwise differences in topographic connectivity scores between ROIS, we performed Holm–Bonferroni correction of P values to account for the number of tests conducted. This was implemented using the emmeans R package⁶⁴. We note that, given our n (174) and alpha level (α = 0.05), the analyses described are powered to detect a Cohen’s d_z in excess of 0.149, indicating that only very small effect sizes could remain undetected by such tests.

Thresholding of model performance

To distinguish between signal and noise in our parameter estimates, we used several strategies to threshold according to model performance. For visualization and analysis of group-level results (Fig. 1e), we thresholded according to vertex locations that have significant topographic connectivity according to a one sample t-test (see above). Any areas in which the group-level topographic connectivity is significantly greater than 0 are shown on the plot (α = 0.05). This measure is more conservative than R², as it is a cross-validated performance measure explicitly referenced against a null model. We note that this thresholding procedure yields regions previously defined as being somatotopic and parameter estimates from these regions agree well with conventionally defined estimates derived from exogenous stimulation (Extended Data Fig. 5e–h).

over, all somatotopic regions analysed in this manuscript survived multiple-comparisons correction using threshold-free cluster enhancement (TFCE), which controls for family-wise error while accounting for spatial correlations in the data⁶⁵. Rather than applying an initial cluster-forming threshold, TFCE integrates evidence for cluster-like structure across all possible thresholds by weighting both the height of the statistic and the spatial extent of signal support. Specifically, topographic connectivity scores were first converted into TFCE scores, which were then compared against a null distribution generated by random sign-flips across participants. For each permutation, the TFCE transformation was recomputed and the maximum TFCE value retained, yielding a null distribution of 2,000 maximum scores. The observed TFCE scores were then conservatively evaluated against this null distribution, with corrected P values derived from the corresponding quantiles (α = 0.01, two-tailed).

For individual-participant outcomes, we used procedures that mirrored those of the HCP 7 T retinotopy pipeline⁶⁶. For each modality-split variance-explained score (visual, somatosensory), we determined a threshold by fitting a Gaussian mixture model with two Gaussians to the distribution of variance explained values across vertices (excluding source regions) and then identified the value at which the posterior probability switches from the Gaussian with the lower mean to that with the higher mean. The interpretation of this procedure is that the Gaussian with a lower mean is likely to reflect noise (vertices that are not responsive to visual or somatosensory information), the Gaussian with larger mean is likely to reflect signal (vertices that are sensitive to visual or somatosensory information) and values above the threshold are more likely to reflect signal than noise. This procedure resulted in a visual variance explained threshold of 2.4% and a somatosensory variance explained threshold of 1.9%, which are very close to those used for the HCP retinotopy data (2.2%). The application of this procedure to the HCP average participant yielded a threshold of 10% for the somatosensory modality.

To evaluate the consistency in sensitivity to visual and somatosensory information at the individual level, we summed the number of participants for whom both modalities were above threshold at each vertex location (N^vs). To statistically evaluate the likelihood of obtaining the observed N^vs under a null hypothesis (no systematic co-localization of tuning across individuals), we performed a permutation-based cluster analysis. First, we decomposed the cortical surface for each hemisphere into 400 LBOEs and used these spatial profiles as a design matrix for a regression model that predicted the presence of above threshold somatosensory tuning at each cortical location (0 = below threshold, 1 = above threshold). We next used the resulting β weights to predict 1,000 new, surrogate maps of somatosensory tuning by randomizing their sign prior to the dot product with the design matrix. The resulting maps therefore had the same spatial frequency profile as the empirical data but with randomized structure in cortical space.

For each surrogate somatosensory map, we calculated the N^vs at each vertex location and submitted this to a cluster analysis, whereby clusters were defined as contiguous sets of vertices with at least 96 participants above threshold for both modalities at that location (upper binomial limit for n = 174, α = 0.05). We then retained the maximum cluster-wise summed N^vs as a test statistic and concatenated these across surrogate maps to form a null distribution. The same clustering procedure was performed on the empirical data and P values were obtained by calculating the proportion of the null distribution that was lower than the summed N^vs in each empirical cluster.

The resulting data are shown in Extended Data Fig. 7a,b. Four bilateral clusters were detected, the largest of which encompassed dorsolateral visual cortex and parts of the superior parietal lobule. Other, smaller clusters were observed in the superior temporal lobe and frontally, including one overlapping with the frontal eye field. The profile of N^vs also revealed a small ‘hotspot’ of reliably above-threshold tuning in posterior parietal cortex, which may correspond to the visuotactile map described previously²⁸ (Extended Data Fig. 7b–e).

Connective-field sampling extent

The approach reported here differs from classical connective-field estimation of a Gaussian centre (V₀) and an explicit size (σ) parameter. Our model removes this constraint and allows flexible estimation of more complex spatial patterns, requiring us to develop a metric to approximate sampling extent.

To provide such estimates, we calculated the median geodesic distance from the peak of each connective-field profile at which it is above its half-maximum. Note that such a computation ignores data from the opposite hemisphere to the peak, as cortical hemispheres are not contiguous surfaces. These quantifications are shown in Extended Data Fig. 10. When calculating this metric for V1 connective fields, we observe coherent increases in V1 sampling extent with distance from V1 that mirror those derived from classical connective-field models/pRF mapping¹² and are consistent with the sizes expected from previous video-watching-derived estimates¹⁵.

Similarly, for S1 connective fields, we observed a strong positive relationship between S1 sampling extent and geodesic distance from S1 in frontal and parietal directions, with weaker relationships in the medial and insular directions. This pattern of results aligns well with somatotopic mapping studies⁶⁷, which demonstrate hierarchical-gradient-like decreases in bodily selectivity. This method of estimating connective-field sampling extent is validated by mirroring organizational hallmarks consistent with previous empirical studies.

Cortical coverage of somatotopic connectivity and relation to functional localizer

The extent of cortical coverage was assessed via a standard bootstrapping procedure. Individual-participant topographic connectivity scores were resampled with replacement 10,000 times to generate resampled datasets with random samples of participants. For each resampled dataset, we quantified the percentage of voxels within each somatosensory ROI with topographic connectivity scores significantly greater than zero. In this calculation, note that the source region of the analysis (3b) is excluded. Reported CIs were obtained from the quantiles (2.5% and 97.5%) of the resulting distribution of percentage coverage estimates. The same bootstrapping approach was applied to assess the correlation of somatotopic connectivity scores with functional localizer data from the NSD dataset, for which we used the same group-level t-statistics described above. Using the correlation between somatotopic connectivity scores and the ‘body v all other categories’ t-statistics as a reference, we subtracted the correlation with the corresponding place, face and object t-statistics across 10,000 bootstrapped samples. The resulting distributions of correlation differences were used to compute P values.

Robustness of extrastriate somatotopic maps: permutation test

To evaluate the robustness of extrastriate somatotopic maps, we tested the null hypothesis that out of set somatotopic maps are predictable from maps generated from randomized connective fields, but with preserved autocorrelation structure. Referencing the out-of-set prediction of empirical maps against surrogate instances is important, as the spatial autocorrelation inherent in brain data implies that spatially proximal measurements are likely to be similar, regardless of how they were derived⁶⁸. As such, the statistical significance of agreement between maps is likely to be inflated and violate independence assumptions. Thus, rather than relying on the statistical significance of these empirical agreement statistics alone, they require benchmarking against surrogate data that quantifies the statistical expectations under a null hypothesis.

To this end, we first used the somatotopic map estimated for the cutout region in Fig. 4a from one split-half of participants to predict the corresponding data from the other split-half. The resulting R² value was retained as an empirical test statistic. To generate a null distribution of these statistics, we generated 10,000 ‘surrogate’ homuncular maps from each split-half of participant data. These were generated by taking the estimated b* corresponding to each of the LBOEs of the S1 subsurface, randomizing their sign and recomputing the S1 connective field. This manipulation generates randomized connective fields that preserve the same amplitude spectra (distribution of energy across frequency) as the empirical data. For each surrogate dataset, we then computed its performance in predicting the out of set empirical somatotopic map and retained the proportion of these statistics that exceeded the empirical value as a P value. This process was repeated for the second participant split and the resulting P values were summed to obtain a final measure of the probability of obtaining the empirical statistic under the null hypothesis.

Visual body-part selectivity estimates

To estimate a map of visual body-part selectivity, we leveraged data from the NSD, also collected at 7 T (ref. ⁶⁹). Specifically, we used the denoised single trial β-estimates from the final 12 runs of data of all 8 participants. This corresponded to 9,000 functional volumes, each of which included voxel-wise estimates of the response to an image from the Common Objects in Context (COCO) dataset⁷⁰. Using Connectome Workbench commands, the cortex-wide single-trial β-estimates were nearest-neighbour resampled from fsaverage space to the same 59,000 vertex-per-hemisphere surface format as the HCP data.

We next used a corpus dataset of estimated body-part keypoints within each image of the COCO dataset, which were generated by Openpose⁷¹, a convolutional neural network based pose-estimation toolkit. Openpose detects the location of 17 different keypoints (nose, left eye, right eye, left ear, right ear, left shoulder, right shoulder, left elbow, right elbow, left wrist, right wrist, left hip, right hip, left knee, right knee, left ankle, right ankle). Thus, each image in the COCO dataset is associated with 17 binary variables that codes the presence of each keypoint for every human entity within the image. Critically, the subset of COCO images used in the NSD dataset were spatially cropped relative to the original versions for which the keypoints were computed. We therefore recoded keypoints that were coded as present in the original COCO images but resided outside of the NSD crop-box as being 0 (absent). For each image and body part, we calculated the average of the binary variable for each keypoint across entities to give an estimate of the frequency with which the body part was present within entities within the image.

Next, we converted these scores into a regressor that explicitly coded selective responses for each body part. For each body part, we calculated a selectivity score defined as follows:

In this calculation, for example, an image with the presence of an ankle and the absence of all other body parts generates the highest score for the ankle selectivity regressor. Conversely, the score will be implicitly penalized as a function of the number of other (non-ankle) body parts that are visible. These regressors for each body part were stacked into a design matrix. This formed the basis of a forward model of visual body selectivity, of which the parameters were estimated by ridge regression. The model was trained on 10 of the runs of data through k-fold cross-validation and was tested on the final 2. For each voxel, body part preference was defined as the dot product of the resulting β weights and their ordinal position in the S1 homunculus (ankle to nose) providing a continuous map of visual body part selectivity along a similar toe–tongue axis as the somatotopy data.

Searchlight analyses: permutation test

Within the cutout region in Fig. 4 we defined geodesic ‘chunks’ of cortex that were centred at each vertex with a radius of 8 mm. To generate empirical statistics, within each one of these chunks we computed the correlation between the somatotopic map shown in Fig. 4 and the target data (vertical visual field position in retinotopic map or visual body part selectivity map). To generate a null distribution of these statistics, we leveraged the same 10,000 phase-scrambled surrogate homuncular maps (see the ‘Robustness of extrastriate somatotopic maps: permutation test’ section) and, for each one, we calculated the corresponding correlations with the target data in each chunk. This distribution of local chunk-wise correlations obtained across all surrogate somatotopic maps served as our null distribution of local correlations. P values for the correlations within each empirical chunk were obtained as the probability of obtaining such extreme statistics from this null distribution. Note that, for the analysis of the retinotopy data, we excluded chunks for which the range of the estimated visual field positions was less than 1 DVA and therefore had little retinotopic variation. The resulting P values were then projected into the spatial locations of their corresponding chunk and the data were then averaged across hemispheres to produce the data in Fig. 5e,i. Note that as the chunks contained partially overlapping data, the data in Fig. 5 show the lowest P value obtained at each vertex location. In addition to the results reported in the main text, we performed additional analyses that correlated the eccentricity parameter of the retinotopy data with the somatotopic map. This revealed a region overlapping with IPS0 and IPS1 wherein more foveal locations were tuned to facial features and more eccentric locations tuned to limbs (Extended Data Fig. 8).

Alternative model: field-based connective-field model

There is evidence that S1 is not a continuous somatotopic map, but consists of discrete body-part fields, defined on the basis of resting state connectivity, myelin and functional data¹⁷. Accordingly, a model that assumes discontinuous connectivity at the boundary of such fields, rather than continuous connectivity along the 3b surface, may provide a viable alternative account of the data. To explicitly test this organizing influence of body part fields, we compared our full connective-field model that uses all of 3b as a source region to 4 alternative connective field models (Extended Data Fig. 8e), each with restricted source regions corresponding to the lower limb, trunk, upper limb and face fields, following the definitions described in the ‘Analysis of subfields within the S1’ section. To ensure validity of such a comparison, we determined the number of LBOEs in each of these restricted source regions sufficient to reconstruct 4 mm Gaussian connective fields at near-ceiling performance (determined by the minimum R² being above 0.98 across vertex locations). This implied 70 LBOEs each for the lower limb, trunk and face fields, and 50 for the upper limb field. These alternative models were then fit using identical procedures described for the full model. For each vertex location, we then selected the cross-validated somatosensory R² from the best performing restricted model and subtracted it from that of the full model, yielding a ΔR². These outcomes are shown in Fig. 4e,f.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.